El totiente

El totiente es un elemento de la matematica discreta muy util por sus propiedades para el cifrado y descifrado de mensajes en criptosistemas de clave publica, como RSA. El totiente es una funcion que determina la cantidad de coprimos para un entero positivo. Suponga el subconjunto del anillo modular entero de N:

$(\mathbb{Z}/N)^{*} = \set{m \in \mathbb{N}: 1 \leq m \leq n, gdc(m,n)=1}$

El totiente es la cardinalidad del subconjunto:

$\phi (N) = |(\mathbb{Z}/N)^{*}|$

Observar que el conjunto \((\mathbb{Z}/N)^{*}\) es el conjunto de todas las unidades modulo N (unidad: elemento invertible), es decir es un campo en si mismo. Ademas tenemos la formula de euler para el totiente que es:

Totiente: Si \(p_{1},p_{2},...,p_{k}\) son todos los diferentes primos que dividen a N, entonces:

$\phi (N) = n \cdot (1 - \frac{1}{p_{1}}) \cdot (1 - \frac{1}{p_{1}}) \cdot ... \cdot (1 - \frac{1}{p_{k}})$

Propiedad multiplicaviva:

$\phi (abc) = \phi (a) \cdot \phi (b) \cdot \phi (c)$

Propiedad factores primos repetidos: Considere \(n = p1^{e1} \cdot p2^{e2} \cdot ... \cdot pk^{ek}\)

$\phi (n) = \phi (p1^{e1}) \cdot \phi (p2^{e2}) \cdot ... \cdot \phi (pk^{ek})$

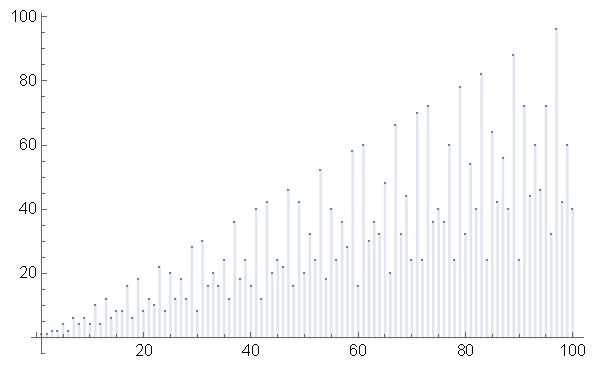
La grafica de los primeros 100 totientes es la siguiente:

Ataques que usan el totiente:

1) Recuperar p y q si se tiene p+q y pq: Dado que el totiente de un numero compuesto por numeros primos se puede calcular como \(\phi(n) = (p - 1) \cdot (q - 1)\), podemos hacer el siguiente analisis:

$(p - 1) \cdot (q - 1) = pq - (p+q) + 1 = \phi (n)$

Y ademas podemos colocar estos datos en una ecuacion cuadratica:

$ x^{2} - x(p+q) + pq = 0$
$(x-p)(x-q)=0$

Por lo tanto usando la formula resolvente podemos encontrar los valores enteros que hacen solucion de esta ecuacion y corresponden a p y q.

2) Descifrar un mensaje dado un multiplo del totiente: si tenemos la clave publica e2 de alguna persona y nosotros tenemos e1 y d1 con e2 y e1 generados con los mismos primos p, q, podemos descrifrar el mensaje de e2 sin factorizar N o tener p y q.
Lo primero que debemos hacer es generar el un multiplo del totiente, esto puede hacerse con:

$k \cdot \phi(N) = e1 * d1 - 1$

Luego generamos una inversa de e2 modulo \(k \cdot \phi(N)\) y la usamos de igual manera que usariamos la clave d2.