La criba de Eraestotenes
Planeo hacer una serie de posts donde se explique la generacion de numeros primos. Ya que a lo largo de la historia se han descubierto diversos metodos para generar numeros primos, desde la lejana grecia donde Eraestotenes de Cirene invento la famosa Criba, hasta los complejos metodos de hoy en dia que mezclan fenomenos fisicos de extrema entropia como las fluctuaciones de temperatura en un procesador con el test de primalidad de Miller - Rabin. Esta serie para que quede ordenada y se entienda de mejor manera la ire escribiendo en orden historico, partiendo en este post con la Criba de Eraestotenes.
En un principio casi de manera natural si se piensa como generar numeros primos, el primer metodo que se viene a la mente es la fuerza bruta. El cual se podria definir en los siguientes pasos:
Algoritmo de fuerza bruta para generar numeros primos.
La implementacion en python del algoritmo para generar numeros primos por fuerza bruta es:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
a = int(input("Ingrese el limite sobre el cual no quiere generar mas numeros el menor valor que puede ingresar es 2 : "))
i = 2 #Es el numero para el cual probaremos si es primo
arreglo_primos = [] #Es la estructura donde iremos guardando los primos que encontremos
while i <= a:
k = 2
while i >= k:
if i == k:
arreglo_primos.append(i)
i = i + 1
break
if i % k == 0:
i = i + 1
break
k = k + 1
print(f"Los primos generados hasta {a} son {arreglo_primos}")
Para tener una idea de lo eficiente que es este algoritmo podemos generar una grafica de cuanto se demora en generar los numeros primos si le pasamos como a una potencia de 2 es decir: \(a = 2^{n}\) donde \(n = 1, 2, 3, .. , 15\) . La implementacion de esta idea en python se muestra a continuacion:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
import time
def GeneradoraRendimiento(n_maximo):
resultados = []
n = 1
while n <= n_maximo:
a = pow(2, n)
#Iniciamos la medicion del tiempo
inicio = time.time()
i = 2 #Es el numero para el cual probaremos si es primo
arreglo_primos = [] #Es la estructura donde iremos guardando los primos que encontremos
while i <= a:
k = 2
while i >= k:
if i == k:
arreglo_primos.append(i)
i = i + 1
break
if i % k == 0:
i = i + 1
break
k = k + 1
#Finalizamos la medicion
fin = time.time()
#Calculamos y guardamos el resultado en segundos
resultado = (a, fin - inicio)
resultados.append(resultado)
n += 1
return resultados
#Debe ser un valor entero mayor a 1
n_maximo = int(input("Ingrese el n maximo: "))
resultados = GeneradoraRendimiento(n_maximo)
print(resultados)
Y lo que obtenemos son los siguientes 15 primeras potencias de 2 como valores de a con sus respectivos tiempos de ejecucion en segundos.
$ python generador_rendimiento_fuerza_bruta.py
Ingrese el n maximo: 15
[(2, 0.0), (4, 0.0), (8, 0.0), (16, 0.0), (32, 0.0), (64, 0.0), (128, 0.0), (256, 0.0019352436065673828), (512, 0.010740995407104492), (1024, 0.024410486221313477), (2048, 0.049469947814941406), (4096, 0.18018770217895508), (8192, 0.8318197727203369), (16384, 2.600992441177368), (32768, 9.908718824386597)]
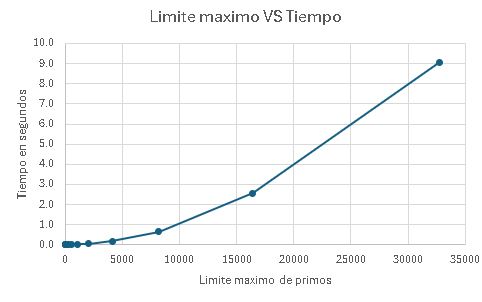
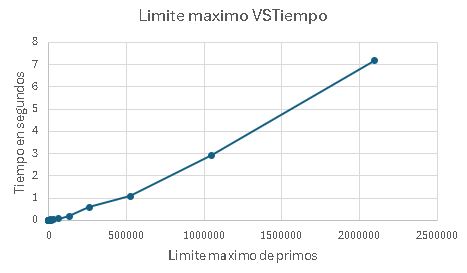
Ahora podemos trabajar estos datos pasandolos a excel en formato csv y hacer la grafica que se muestra a continuacion:
Donde se ve que el algortimo de fuerza bruta tiene un crecimiento potencial, lo cual no es muy bueno. Ahora es turno de que veamos La criba de Eraestotenes y estudiemos porque es mejor que la fuerza bruta.
La criba de Eraestotenes
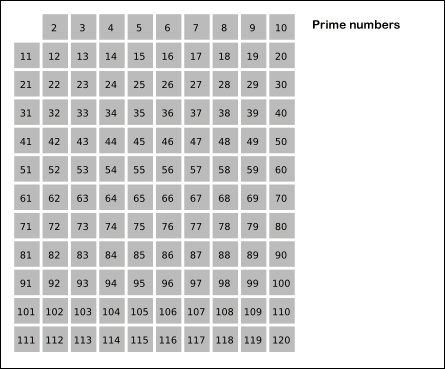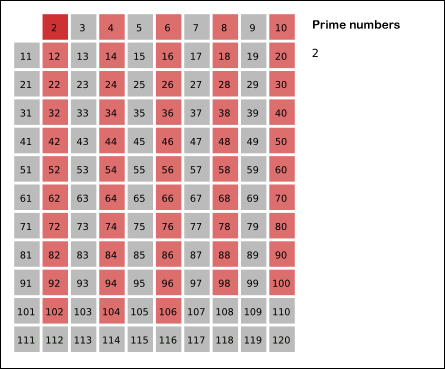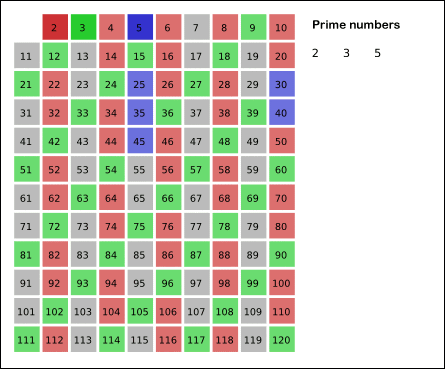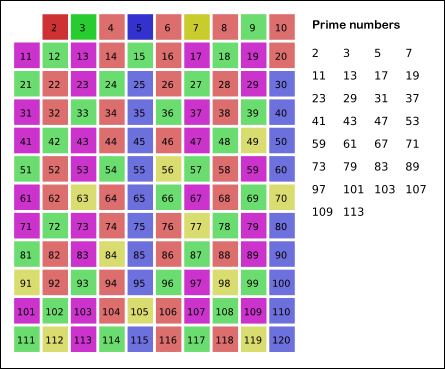
La criba de Eratóstenes es un algoritmo que permite hallar todos los números primos menores que un número natural dado. Se forma una tabla con todos los números naturales comprendidos entre 2 y n, y se van tachando los números que no son primos de la siguiente manera: Comenzando por el 2, se tachan todos sus múltiplos; comenzando de nuevo, cuando se encuentra un número entero que no ha sido tachado, ese número es declarado primo, y se procede a tachar todos sus múltiplos, así sucesivamente. El proceso termina cuando el cuadrado del siguiente número confirmado como primo es mayor que n. A continuacion se muestra una animacion de la criba para extraer los primos de los primeros 120 numeros naturales, en la animacion se observa que deja de calcular multiplos cuando llega al 11 ya que \(11^{2} = 121 > 120\).
Porque se hace hasta que el siguiente primo cuyo cuadrado es mayor que n?
Existe un teorema en la teoria de numeros que dice: Todo numero compuesto \(k\) es divisible por un primo y este es menor o igual a \(\sqrt{k}\).
Demostracion:
Sea \(K\) un numero compuesto y \(P\) el menor divisor mas grande que 1. En otras palabras \(P\) es el menor primo que divide a \(K\).
Del enuciado anterior podemos calcular \(Q = \frac{K}{P}\) donde q es un numero natural y \(Q \geq P\) pues \(Q\) tambien es un divisor de \(K\) y dijimos que \(P\) era el menor de todos los divisores de \(K\)
Ademas se tiene que \(P \leq \sqrt{K}\) ya que por contradiccion podemos demostrar que si p fuera mayor que \(\sqrt{k}\) tendriamos que:
\[K = P\cdot Q > \sqrt{K} \cdot Q \geq \sqrt{K} \cdot P > \sqrt{K} \cdot \sqrt{K} = K\]Es decir \(K > K\) lo cual es una falacia por la propiedad de orden de los numeros naturales. Por lo que la hipotesis \(P \leq \sqrt{K}\) es correcta . Quedando demostrado el teorema.
La aplicacion que hacemos de este teorema en este problema es que cuando encontremos un primo \(i\) con el que sobrepasemos \(\sqrt{n}\) por nuestro metodo de descarte ya habremos tapado todos los numeros compuestos entre [2, k] por lo que todos los numeros que nos queden seran primos y podemos agregarlos sin mas. Ahora en la criba usamos este teorema pero elevamos al cuadrado ambas partes de su conclusion para que sea mas facil de trabajar y tambien sea mas general por lo que la condicion \(i > \sqrt{n}\) nos queda \(i^2 > n\).
Implementacion de la Criba de Eraestotenes
La siguiente funcion SmallPrimeList implementa la criba para generar numeros primos.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def SmallPrimeList(limite_maximo):
#Primero generamos una lista con todos los numeros
todos_los_numeros = [i for i in range(0, limite_maximo+1)]
#Este es el primer primo que tendra la lista
i = 2
#Implementamos el algoritmo de eliminacion
while pow(i,2) <= limite_maximo:
k = i
while k * i <= limite_maximo:
todos_los_numeros[k * i] = -1
k = k + 1
#Buscamos el siguiente numero primo
for numero in todos_los_numeros[i + 1:]:
if numero != -1:
i = numero
break
#Extraemos solo los numeros que quedaron los cuales son todos los primos
primos = []
for numero in todos_los_numeros[2:]:
if numero != -1:
primos.append(numero)
return primos
print(SmallPrimeList(120))
Ahora igual que con el codigo anterior podemos generar el rendimiento con el siguiente codigo, notar que con la criba podemos poder como limite maximo 2^21 y encuentra los primos con facilidad.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
import time
def SmallPrimeList(limite_maximo):
#Primero generamos una lista con todos los numeros
todos_los_numeros = [i for i in range(0, limite_maximo+1)]
#Este es el primer primo que tendra la lista
i = 2
#Implementamos el algoritmo de eliminacion
while pow(i,2) <= limite_maximo:
k = i
while k * i <= limite_maximo:
todos_los_numeros[k * i] = -1
k = k + 1
#Buscamos el siguiente numero primo
for numero in todos_los_numeros[i + 1:]:
if numero != -1:
i = numero
break
#Extraemos solo los numeros que quedaron los cuales son todos los primos
primos = []
for numero in todos_los_numeros[2:]:
if numero != -1:
primos.append(numero)
return primos
def GeneradoraRendimiento(n_maximo):
resultados = []
n = 1
while n <= n_maximo:
a = pow(2, n)
#Iniciamos la medicion del tiempo
inicio = time.time()
SmallPrimeList(a)
#Finalizamos la medicion
fin = time.time()
#Calculamos y guardamos el resultado en segundos
resultado = (a, fin - inicio)
resultados.append(resultado)
resultado = f"{a};{fin - inicio}"
print(resultado)
n += 1
#Debe ser un valor entero mayor a 1
n_maximo = int(input("Ingrese el n maximo: "))
GeneradoraRendimiento(n_maximo)
La grafica de rendimiento de este algoritmo es mucho masa lineal en su crecimiento y se ve asi:
Conclusion
Si se va necesita generar listas de numeros primos no mayores a numeros como 2^25 la criba de eraestotenes es una buena opcion. Pero en criptografia los numeros de esas dimensiones aun siguen siendo muy pequenos y no pueden garantizar la seguridad de un criptosistema por lo que se usan otros metodos para generar esos numeros primos.